Dokumendid > Keemia > Üldkeemia > Teoreetiline keemia I kordamisküsimuste vastused

KORDAMISKÜSIMUSED

Aines Teoreetiline keemia I

Õppeaasta 2012/13 sügissemester

Kvantmehaanika põhiprintsiibid. De Broglie' printsiip. Kvantmehhaaniline süsteem, selle lainefunktsioon. Operaatorid kvantmehhaanikas. Heisenbergi määramatuse printsiip.

1. De Broglie' printsiip. Igale materiaalsele osakesele massiga m ning

kiirusega v vastab laine pikkusega λ. Seejuures kehtib lihtne seos mv=h/λ

(h: Plancki konstant.)

2. Igat elementaarosakestest koosneva süsteemi olekut iseloomustab lainefunktsioon Ψ , mis annab osakeste konfiguratsiooni selles olekus. Lainefunktsioon Ψ ei vasta otseselt ühelegi füüsikaliselt mõõdetavale suurusele. Lainefunktsiooni ruut (korrutis kaaskompleksse funktsiooniga) on võrdeline osakese leidmise tõenäosuse tihedusega (antud koordinaatide väärtuste korral).

Lainefunktsioon peab olema ühene, lõplik, pidev ning määratud kogu argumentide skaala ulatuses. Lõpliku väärtusega peab olema ka tema ruudu integraal üle kogu ruumi.

Kui osakest iseloomustab antud olekus lainefunktsioon Ψ , siis on ta selles

olekus kirjeldatav ka funktsiooniga kus c on suvaline arvuline konstant. C on valitud nii, et

(normeeritud lainefunktsioon).

3 . Kvantmehaanikas on operaatorid; mida lainefun rakendades saab teada kvantmeh süsteemi mingi füüsikalise omaduse (nt energia). Operaatori O abil on süsteemi lainefunktsioon Ψ leitav järgmisest võrrandist (omaväärtusülesandest)

O on arvuline suurus (operaatori O omaväärtus antud olekus), mis iseloomustab mingit vaadeldava süsteemi mõõdetavat omadust. Igale O_i -le vastab 1 Ψ_i

4. Heisenbergi määramatuse printsiip: Paarsete dünaamiliste suuruste f ja g minimaalsete ebatäpsuste korrutis ei saa olla väiksem etteantud universaalsest konstandist:

(nt energia-aeg või impulss-asukohakoordinaat). Asukoha ja impulsiga seotud määramatuse printsiip kehtib vaid sama ruumikoordinaadi suunas määratud muutujate (näiteks x ja px) korral.

Seega teades täpselt osakese asukohta ruumis, puudub igasugune informatsioon tema impulsi kohta

Operaatorid ja omaväärtusülesanne. Kvantmehhaaniliste operaatorite omadused. Maatriksid ja vektorid kvantmehaaniliste objektide matemaatiliste mudelitena.

Operaatorid on matemaatilised eeskirjad, mille tulemusel mingi funktsioon osutub korrutatuks teatud konstantse arvuga (omaväärtus). Kvantmehhaanilised operaatorid on :

LINEAARSED

SUMMA ON KOMMUTATIIVNE

JA ASSOTSIATIIVNE

KORRUTIS võib olla MITTEKOMMUTEERUV

HERMIITSED

Eksisteerib ühikoperaator, mille toimel fun jääb iseendaks

HERMIITSE OPERAATORI kõik OMAFUNKTSIOONID MUUDUSTAVAD TÄIELIKU ORTONORMEERITUD FUN SÜSTEEMI. St suvalist fun saab esitada lin kombinatsioonina omafunktsioonidest

fun on ortonormeeritud kui

Kui operaatorid on kommuteeruvad, siis on neil ühine täielik ortonormeeritud omafun komplekt.

Lainefunktsioonide matemaatiliseks mudeliks on vektor; operaatorite mat mudeliks maatriks. Sest ka vektorruumi baas on lin sõltumatute vekt kogum, mille lin komb kaudu on avaldatav suvaline vektor antud ruumis.

Omaväärtusülesande lahendamisel on vaja leida suurused, mis sõltuvad 2 indeksist ja neid suurusi on mugav esitada ruutmaatriksiteda. Pealegi kattuvad mx omadused (suures osas) operaatorite omadega.

Schrödingeri võrrand. Variatsioonimeetodid Schrödingeri võrrandi lahendamiseks. Variatsiooniprintsiip. Häiritusmeetodid Schrödingeri võrrandi lahendamiseks.

Schrödingeri võrrand on lainemehaanika keskseks võrrandiks. Schr võrrand on mõeldud kvantmehh osakese või osakeste süsteemi koguenergia leidmiseks E=T+V Operaatorkujul on

Variatsiooniprintsiip väidab, et suvalise lainefunktsiooni ϕ abil võrrandist arvutatud koguenergia keskväärtus E_i pole kunagi väiksem (negatiivsem) kui hamiltoniaaniga iloomustatud süsteemi tõeline energia põhiolekus E₀

Variatsioonimeetod id: lainefunktsiooni lähendina kasutatakse mingit proovifunktsiooni, mis esialgu sisaldab ta mitteteadaolevaid parameetreid. Leitakse parameetrite sellised väärtused, mille korral süsteemi energia on minimaalne (Vastavalt printsiibile süsteemi energia parima lähendiga antud lainefunktsiooni korral). Proovifunktsioon võib olla põhimõtteliselt suvalise matemaatilise kujuga, (peab rahuldama lainefunktsioonidele esitatavaid nõudeid). Enamasti valitakse see funktsioon f lineaarkombinatsioonina mingitest teadaolevatest funktsioonidest, mis ei moodusta täielikku süsteemi ning enamasti pole ka ortogonaalsed. Loe lisaks ka sekulaarvõrrandi, kattumismx kohta

Häiritusmeetodid : Uuritava süsteemi hamiltoniaan H jaotatakse kaheks osaks:

Häirimata süsteemi hamiltoniaan ja häirimata süsteemile vastav hamiltoniaan. Lainefun ja energia arendatakse ritta parameetri järgi. Read asendatakse põhivõrrandisse ja nende võrrandite järjestikusel lahendamisel saadakse vastavat järku parandused lainefun ja energiale.

Mitme kvantmehhaanilise osakese süsteemi lainefunktsiooni kuju. Sõltumatute osakeste mudel bosonite ja fermionide korral. Slateri determinant.

Elektriliselt laetud n osakese süsteemi hamiltoniaan sisaldab lisaks kin energia operaatorile ka osakeste elektrostaatilise vastasmõju potentsiaali vastavalt Coulomb'i seadusele. Taoline operaator sõltub kõigi osakeste koordinaatidest ja see on matemaatiliseks analüüsiks liiga keeruline. Sellepärast võeti kasutusele sõltumatute osakeste mudel, mille järgi esitatakse n osakesest koosneva süsteemi lainefun ligikaudse korrutisena funktsioonidest, mis sõltuvad ainult 1 osakese koordinaatidest.

Elektroni igale ruumiorbitalile vastab 2 kogulainefun ehk spinnorbitali.

Bosoneid saab kirjeldada lihtsa Hartree korrutisega; fermione ei saa, kuna nende puhul peab kehtima antisümmeetria

Vajalikke antisümmeetrilisi lainefun saab moodustada Hartree korrutiste kombinatsioonidest, kuid see on suurema osakeste arvu korral tüütu. Suuremate osakeste arvu korral kasutatakse seega lainefunktsiooni esitamiseks Slateri determinanti. Slateri determinant põhineb lihtsal reeglil, et n osakese lainfun on avalduv n järku determinandina, mille veeru indeks vastab üheelektroonse spinnorbitali indeksile ja rea indeks vastab osakese järjekorranumbrile.

Aatomühikute süsteem. Energia standardolekud.

Aatomühikute defineerimisel on põhiühikud (mass, pikkus, laeng) avaldatud elektroni omaduste kaudu. Sellise süsteemi kasutamist põhjustab eelkõige kaks asjaolu.

SI-süsteemi mõõtühikuid kasutades oleks arvud väga väiksed ja kvantkeemilised arvutused nõuavad põhisuuruste suurt täpsust (8-9 tüvenumbrit). Esitades arvutustulemused aatomühikute süsteemis, ei pea tegema ümberarvutamisi elektroni omaduste või universaalsete konstantide väärtuste edasisel täpsustamisel.

Teiseks lihtsustab aatomühikute süsteemi kasutamine oluliselt Schrödingeri

võrrandi kuju

Energeetiliste suuruste arvulisel esitusel lähtutakse alati mingist energia nulltasemest. Standardolekuks nimetatakse uuritavat objekti sellisel tasemel.

Füüsikaline standardolek : vaakum. Aatomi/molekuli energia selle standardoleku suhtes koosneb nendes olevate elementaarosakeste seisumassile vastavast energiast, kineetilisest energiast ja potentsiaalsest energiast

Kvantkeemiline standardolek: üksteisest isoleeritud elektronid ja aatomituumad. Aatomi või molekuli energia selle standardoleku suhtes koosneb elektronide ja aatomituumade kineetilise ja potentsiaalse energia summast . Sch võrr lahendamisel saadakse süst koguenergia just selle st oleku suhtes.

Keemiline standardolek . Keemiliseks standardolekuks on isoleeritud aatomid. Seega on mistahes aatomi energia selle standardoleku suhtes võrdne nulliga. Molekuli energia avaldub aga kõigi temas olevate keemiliste sidemete dissotsiatsioonienergiate summana.

Termodünaamiline standardolek : keemilised elemendid 25°C ja 1 atm rõhu juures Ühendite molaarsed energiad termodünaamilise standardoleku suhtes on samased nende tekkeentalpiatega.

Vesinikusarnase aatomi teooria. Elektroni lainefunktsiooni radiaalne ning sfääriline osa vesinikusarnases aatomis. Aatomorbitalid.

Vesinikusarnasteks aatomite korral on kogu lainefunktsioon võrdne elektroni lainefunktsiooniga. Üldiselt võttes on tegu ühe negatiivselt laetud elektroniga aatomituuma elektrostaatilises tsentraalsümmeetrilises väljas. Selle Sch võrr lahendamisel kasutatakse sfäärilisi koordinaate ja tänu sellele saab Sch võrrandi kirjutada 2 sõltumatu diferentsiaalvõrrandina, millest üks sõltub raadiuskoordinaadist ja teine sfäärilistest nurkadest.

Sfäärilisi muutujaid sisaldava dif võrrandi lahenditeks on sfäärilised harmoonikud, mis sõltuvad 2 kvantarvust : orbitaalne l=0,1,2... ning magnetiline m=-l,-l+1,...,l-1, l. Orb kvantarv määrab ära nulltasandite arvu. Sfäärlised osad on universaalsed ja ei sõltu aatomi tüübist

Kujud: ÄRA UNUSTA + ja – märke!!!

Radiaalse lainefun lahendid sõltuvad lisaks orbitaalsele ka peakvantarvust n; n=1,2,3...Radiaalse võrrandi lahendamisel saab ka koguenergia vääruse, mis sõltub ainult peakvantarvust n. Radiaalsed osad on igale aatomile spetsiifilised (kuid ei erine siiski väga palju). Nullkohtade arv on määratud N_p=n-l-1

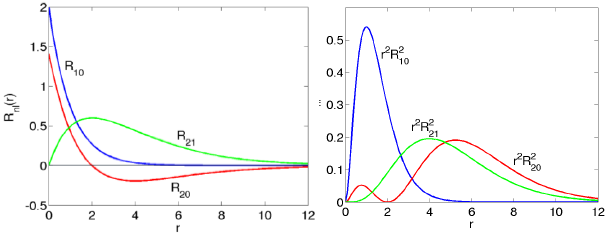
Üheelektroonseid lainefunktsioone, mis kirjeldavad elektronide liikumist, nimetatakse

aatomorbitalideks. Vesinikusarnase aatomi orbitalidega on sarnased ka mitut elektroni sisaldavate aatomite üheelektroonsed lainefunktsioonid. Aaatomorbitalide kuju ning nende omadused mitmesuguste sümmeetriaoperatsioonide suhtes määravad aga neist moodustunud keemiliste sidemete iseloomu ja tüübi. Aatomorbitalid on põhimõtteliselt kahe erinevatest ruumikoordinaatidest sõltuva funktsiooni korrutised:

Kooskõlalise välja meetod mitme elektroniga aatomite korral. Hundi reeglid.

Võib olla kirjutan sellest ka, miks SCF vajalik on?

Valitakse mingisugused lähendusfunktsioonid ψ_i iga elektroni orbitali jaoks (näiteks H-sarnased orbitalid).

Lähtudes neist orbitalidest määratakse vastavalt valemile (2.22) keskväärtustatud potentsiaal V(r_i ) iga elektroni jaoks.

Saadud potentsiaal asendatakse üheelektroonsetesse võrranditesse (2.23) ning nende lahendamisel saadakse uus orbitalide komplekt ψ_i

Vastavalt Pauli printsiibile paigutatakse elektronid saadud orbitalidele ning arvutatakse uued potentsiaalid V (r_i).

Võrreldakse antud k-ndal iteratsioonisammul saadud potentsiaale V^(k)(r_i) eelneval iteratsioonil kasutatud potentsiaalidega. Juhul kui potentsiaalid on jäänud praktiliselt muutumatuks, lõpetatakse protseduur ning tulemusena saadud viimased orbitalid ongi kooskõlalised e. Hartree-Focki SCF orbitalid. Vastasel korral jätkatakse iteratsiooni alates punktist 3.

Hundi reeglid :

Erinevatel ruumiorbitalidel asuvad p-elektronid varjestavad üksteist vähem kui samal orbitalil olevad elektronid. Seetõttu paigutavad elektronid ekvivalentsete orbitalidele maksimaalselt eraldi asetatult

Erinevatel ekvivalentsetel ruumiorbitalidel asuvad elektronid püüavad olla paralleelsete spinnidega.

Molekulide hamiltoniaan. Molekulide lainefunktsiooni esituse võimalused. MO meetod. VB meetod. CI meetod. MC SCF meetod.

Molekulide näol on tegemist kvantmehaaniliste süsteemidega, mis koosnevad mitmest elektronist ja aatomituumast. Vastavalt sellele on molekuli hamiltoniaan jagatav järgmisteks osadeks: elektronide liikumisega seotud osa: tuumade liikumisega seotud osa: elektronide ja tuumade vahelise vastasmõjuga seotud osa:

Valentssidemete (VB-) meetod .

Molekuli lainefunktsioon leitakse lineaarkombinatsioonina Slateri determinantidest. Elektronide lainefunktsioonidena kasutatakse naaberaatomite valentskihi aatomorbitale.

Molekulaarorbitalide (LCAO MO) meetod .

Molekuli lainefunktsioon on antud ühe determinandina mis harilikult vastab molekuli põhioleku elektronkonfiguratsioonile. Üheelektroonsete lainefunktsioonidena kasutatakse determinandis molekulaarorbitale (MO): mis on lineaarkombinatsioonid aatomorbitalidest χ k . Kordajad Cik on

variatsiooniparameetriteks kooskõlalise välja meetodil.

Konfiguratsioonilise interaktsiooni (CI) meetod .

Molekuli lainefunktsioon leitakse lineaarkombinatsioonina Slateri determinantidest Φ kus determinandid koosnevad MO-dest. Viimased on enamasti leitud LCAO MO meetodil molekuli põhioleku jaoks, kuid erinevad determinandid vastavad molekuli erinevatele elektronkonfiguratsioonidele (põhiolek, ühe- ja kahekordselt ergastatud olekud jne.)

Multikonfiguratsiooniline kooskõlalise välja (MC SCF) meetod.

Molekuli lainefunktsioon on moodustatud taas determinantidest mis omakorda koosnevad molekulaarorbitalidest Erinevalt CI-meetodist, kus variatsiooniliselt leitakse vaid determinantide ees olevad kordajad D_i , on MC SCF meetodis variatsioonikordajateks nii D_i kui ka MO koefitsiendid c_ik . Meetod on seetõttu täpsem, kuid ühtlasi ka tunduvalt töömahukam. Seetõttu on ta rakendust leidnud suhteliselt väikeste molekulide korral

Valentssidemete meetod. Siduvad ja lõhustavad lainefunktsioonid. Heitler-Londoni meetod ja täiendused sellele – polarisatsioonifunktsioonid, ioonsete struktuuride kaasamine, korrelatsioonifunktsioonid.

Heitler-London

Kahe H aatomi lähendamisel muutub ka süsteemi lainefunktsioon, kuna mitme elektroni süsteemina peab ta rahuldama antisümmeetria tingimust. Ruumiliste orbitalide ja spinnlainefunktsioonide sõltumatuse tõttu saab kogulainefunktsiooni välja kirjutada kahe erineva Slateri determinandina

Esimene lainefunktsioon on sümmeetriline e paarisfunktsioon elektronide vastastikuse ümberpaigutuse suhtes ruumiorbitalidel. Teine on aga antisümmeetriline e. paaritu elektronide

ruumikoordinaatide vahetuse suhtes. H2 molekuli elektroonse energia arvutamisel saadakse 3 tüüpi integraale:

Kuloniline integraal : väljendab elektrostaatilisi interaktsioone süsteemis

Vahetusintegraal: kujutab endast kahe tuuma ja elektroni süsteemi elektrostaatilist energiat,

kui elektronide tõenäosuse tihedus on väljendatud AO-de segakorrutisena (elektron mõlemal orbitaalil korraga)

Kattumisintegraa l:erineb 0-st kuna AO-d pole enam ortogonaalsed.

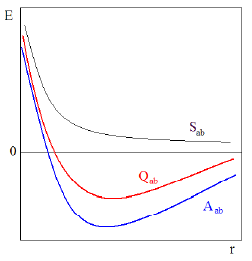
Teostades vastavad asendused elektroonse energia avaldisse saame:

Sümmeetrilisele lainefun vastav energia on madalam kui 2 isoleeritud H aatomi energia; Antisümmeetrilise lainefun vastav energia on aga 2 isol H aatomi omast kõrgem.

Parandused VB meetodile:

polarisatsioonifunktsioonid : Aatomite lähenemisel üksteisele kaotab elektronidele mõjuv potentsiaal sfäärilise sümmeetria. Toimub aatomite elektronkatete polariseerumine, s.t. ka nende laengujaotus pole enam sfäärsümmeetriline. Kuna polariseeriv mõju toimib eelkõige piki tuumiühendavat sirget (keemilist sidet), siis võib seda efekti arvestada molekuli lainefunktsioonis kõrgema kõrvalkvantarvuga orbitalide e. Polarisatsioonifunktsioonide lisamisega. Lugedes Η₂ süsteemis x-teljeks sideme suuna, oleks sellisteks polarisatsioonifunktsioonideks 2 p_x -AO-d.

Ioonsete struktuuride lisamine: aatomite lähenemisel teineteisele Η₂ süsteemis suureneb selliste olekute tõenäosus, kus antud ajahetkel on kaks elektroni ühe tuuma ligiduses. Taoline hetkeline struktuur vastaks siis vormidele Η_a ⁺Η_b ^- ja Η_a ^-Η_b ⁺ .Mõlema H tuuma identsuse tõttu vastab molekuli ioonsetele piirstruktuuridele sümmeetriline lainefunktsioon. Molekuli kogulainefunktsioon on aga summa kovalentsest lainefun ja variatsiooniparameeriga korrutatud ioonsest lainefunktsioonist

korrelatsioonifunktsioonid: Elektronide omavahelise elektrostaatilise tõukumise tõttu ei saa 2 elektroni viibida samas ruumipunktis. Eespool toodud lainefunktsioonid ei arvesta aga sellist piirangut. Seetõttu on vastav elektronide tõukumise destabiliseeriv energia ülehinnatud ning saadud sidemeenergiad liiga madalad. Sellist viga saab parandada korrutades molekuli lainefunktsiooni mingi parandusfunktsiooniga, mis sisaldab ilmutatud kujul elektronide omavahelist kaugust r_12. Kui see kaugus läheneb 0 le siis ka tõenäosus läheneb 0-le. Parandusfun võib olla esitatud matemaatilise reana, mis sis variatsiooniparameetreid.

VB-meetodis on n keemilist sidet sisaldava molekuli lainefunktsioon avalduv 2ⁿ determinandi

kombinatsioonina. Nii on etaani molekuli (milles7 keemilist sidet) kirjeldamiseks VB-meetodil vaja arvestada lainefunktsioonis 2⁷ = 128 determinanti.

Valentsolek ja hübridisatsioon. Hübriidorbitalide kuju ning molekulide geomeetria. Elektronstruktuuride resonants.

Aatomi valentsolek : aatomi olek, milles tema elektronstruktuur on samasugune kui molekulis.

Hübridisatsioon: aatomorbitalide kujuteldav segunemine eesmärgiga moodustada rohkem keemilisi sidemeid.(Selleks, et C aatom saaks metaani molekulis moodustada nelja ekvivalentset sidet, peab ta VB-meetodis kirjeldatud olema nelja ekvivalentse orbitaliga. Sellised orbitalid võib moodustada ühe 2s- ja kolme 2p-orbitali kombinatsioonina ning nad kannavad hübriidorbitalide nime)

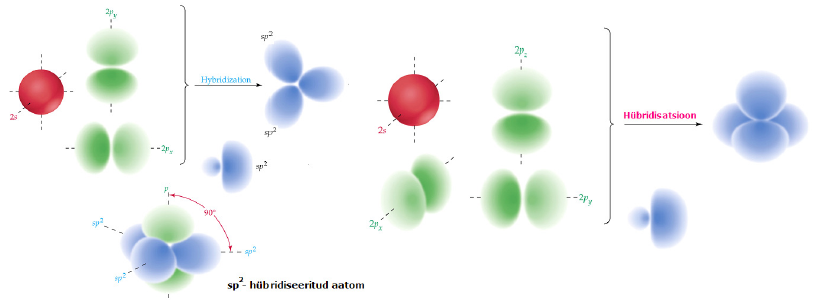sp-hübriid: 2s ja 2p orbitali lineaarkombinatsioonina; igas sp olekus aatomil on 2 hübriidset sp orbitali ja 2 häirimata 2p orbitali jne

sp ja dp on lineaarsed; p^2, ds, d² nurkjas; sp² jt kolmnurkne tasandiline jne

Elektronstruktuuride resonants: resonants on viis kirjendamaks delokaliseeritud elektrone molekulides, kus sidemeid ei saa kirjeldada üheainsa Lewisi valemiga. Sellist molekuli saab esitada mitme resonants piirstruktuuri kaudu. ???

Molekulaarorbitalide (LCAO MO) meetod. Baasi valik LCAO MO meetodis. Minimaalne baas, laiendatud baasid. Hartree-Focki piirenergia. LCAO MO meetodis kasutatavate baasifunktsioonide tüübid. Slateri orbitalid. Gaussi orbitalid.

Molekulaarorbitalide meetodis on molekuli lainefunktsioon antud 1 determinandina, mis harilikult vastab põhioleku elektronkonfiguratsioonile. Üheelektroonsete lainefunktsioonidena kasutatakse determinandis molekulaarorbitale, mis on lineaarkombinatsioonid aatomorbitalidest. Kordajad C_ik on variatsiooniparameetriteks kooskõlalise välja meetodil.

Keskseks probleemiks on selles rittaarenduses baasifun valik. Teoreetiliselt on täpsete MO-de saamiseks vaja kasutada mingit täielikku baasi, mis aga enamasti koosneb lõpmatust hulgast baasifunktsioonidest ning võib veel sisaldada pidevale energeetilisele spektrile vastavat lainefunktsiooni osa. Praktiliste kaalutluste tõttu piirdutakse tavaliselt aga suhteliselt väikese hulga baasifunktsioonidega.

Minimaalseks baasiks nim baasi, kus iga aatomi jaoks molekulis kasutatakse vaid selliseid AO-sid mis vastavad selle aatomi osaliselt või täielikult täidetud elektronkihtidele aatomi põhiolekus. Laiendatud baasideks nimetatakse baase, kus igale AO-le vastab rohkem kui 1 baasifunktsioon:

topelt-dzeeta baas: AO kujutatakse kui 2 sama tüüpi, kuid erineva eksponendinäitajaga baasifun lineaarkombinatsiooni

Polarisatsioonifunktsioonide lisamine: lainefun kvaliteedi parandamiseks kasutada baasis antud aatomi jaoks mittetäidetud elektronkihtidele vastavaid suurema kõrvalkvantarvuga orbitale.

Isegi baasifunktsioonide piiramatu kasvu korral pole LCAO MO meetodiga võimalik saada molekuli tõelise energia väärtust; baasi laiedamisel koondub energia mingile teisele kindlale (kõrgemale) väärtusele, mida nim Hartree-Focki piiriks.(Suurima paranduse toob üleminek DZ baasile; siis ka pol fun)

LCAO MO meetodis kasutatavate aatomorbitalide tüübid:

Slateri orbitalid: Vesinikusarnaste orbitalide lihtsustatud versioon, kus Laguerre'i kaaspolünoom on asendatud lihtsa astmefunktsiooniga. Annab hea kirjelduse aatomi lainefun-le tuumade läheduses või suurel kaugusel. Baasis kasut lineaarkombinatsioone STO-dest. STO-de laiemat kasutamist piirab veel 2elektr integraalide arvutamise keerukus

Gaussi orbitalid : AO esitamine GTO-de kaudu on märksa ebtäpsem kui H-sarnase orb või STO-ga. Samas kuna integraalide arvutamine on GTO-dega tunduvalt hõlpsam, siis kasutatakse neid rohkem. AO-sid võib esitada GTF baasil mitmel viisil: GTO-de baasil saab ritta arendada STO-sid; kontrakteeritud baas; lõhestatud valentsbaas

Kaheaatomiliste (samaaatomiliste) molekulide elektronstruktuur ning füüsikalised omadused.

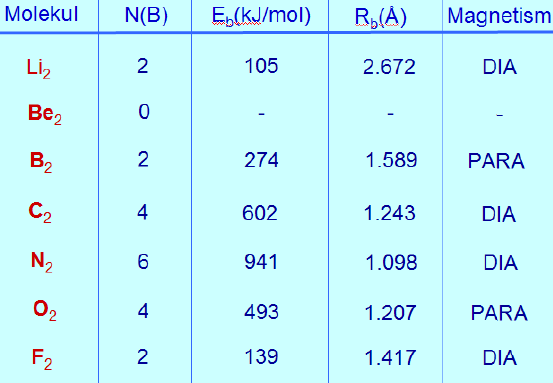Li₂ korral paigutuvad aatomite valentskihi kaks 2s-elektroni siduvale 2σ_g −MO-le. Vastavalt sellele on Li₂ molekul stabiilne ning teda on ka eksperimentaalselt tuvastatud (ca 1% lisandina) Li aurudes. Järgmisena tuleks vaatluse alla Be₂ molekul. Tema neli valentskihi elektroni paigutuvad paarikaupa siduvale 2σ_g −MO-le ning lõdvendavale 2σ_u −MO-le. Kuna MO-de energeetiline paigutus on jällegi sümmeetriline, siis puudub molekulis summaarne siduv efekt ning ta pole püsiv. Be₂ molekuli pole õnnestunud kindlaks teha ka eksperimentaalselt.

Minnes edasi mööda 2. perioodi elemente, järgneb B₂ molekul. Arvutused näitavad, et MO-de järjestus selle molekulis ei vasta päris täpselt joonisel 16 toodud skeemile. Nimelt on 1π_u ja 2π_u-nivood energeetiliselt madalamal kui 3σ_g -nivoo

(Tegemist on lisaefektiga, mis on tingitud sama sümmeetriaga MO-de (antud juhul 2σ ja 3σ) omavahelisest segunemisest. Selle tulemusel ühe MO (2σ ) energia väheneb, teisel aga (3σ ) suureneb )

Seetõttu täituvad enne π -orbitalid. Kuna tegemist on aga kahe identse ( 1π_u 2π_u ) orbitaliga, siis vastavalt Hundi reeglitele paigutub kummalegi neist üks elektron, millede omavaheline spinnide orientatsioon on paralleelne. Seega on B₂ molekul paramagnetiline. Spektroskoopiliselt on B₂ põhiolek detekteeritav tripletina. Järgnevate elementide kaheaatomiliste molekulide korral toimub MO-de täitumine normaalses järjekorras elektronpaaridega. Vaid Ο₂ molekuli osutuvad paardumata elektronidega täidetuks vastavalt 1π_g ja 2π_g orbital. Vastavalt sellele on ka Ο ₂ molekul tripletses olekus ning omadustelt paramagnetiline.

Tabelis toodud andmetest võib täheldada otsest seost molekulides siduvatel MO-del asuvate elektronide ülejäägi ning nende stabiilsuse vahel. Mida rohkem on siduvaid elektrone, seda suurem on ka vastava sideme dissotsiatsioonienergia. Suurema orbitalide vastastikuse kattumise tõttu on siis lühem ka sideme pikkus molekulis

Molekulidevahelise vastasmõjude klassifikatsioon. Solvendiefektide kirjeldamine kvantkeemias. Kooskõlalise reaktsioonivälja (SCRF) ja polariseeritava kontiinumi (PCM, COSMO) meetodid.

Molekulidevahelised vastastikmõjud jagunevad mol vahelise kauguse järgi kolmeks piirkonnaks. I piirkonnas, kus mol üksteisele kõige lähemal, mõjuvad (kasutatakse supermolekuli lähendust)

Kuloniline (elektronide omavaheline tõukumine)

Vahetusenergia (1 elektron korraga 2-l orbitaalil)

II piirkond (süsteemide kirjeldamiseks kasutatakse häiritusteooria meetodeid):

Elektrostaatiline energia

Vahetusenergia

Vahetus-polarisatsiooni energia

Laengu ülekande komponent

III piirkond (süsteemide kirjeldamiseks kasutatakse häiritusteooria meetodeid)

Elektrostaatiline

Polarisatsioonienergia (indutseeritud/dispersioon)

Magnetiline

Aeglustumise efekt

Solvediefekte kirjeldamisel kvantkeemias loetakse lahustumise vabaenergiamuut sõltuvaks lahustisse augu tegemise; elektrostaatiliste; vdW vastasmõjude ja vesiniksidemete moodustumise energiatest

Spetsiifiline solvatatsioon nt H-sidemed; siis kasutatakse supermolekuli lähendust

Mittespetsiifilise solvatatsiooni korral iseloomustatakse solvendiefekte keskkonna dielektrilise konstandiga

Kooskõlalise reaktsioonivälja meetod (SCRF)

Eesmärgiks on lahendada Schrödingeri võrrand juhul kui molekul on asetatud polariseeritavasse dielektrilisse keskkonda. Lahustumise vabaenergia elektrostaatiline komponent saadakse asetades laengu või dipooli kerakujulisse auku. Lahustit vaadeldakse kui ilma molekulideta tervikut, millel on dielektriline konstant ja mis täidab ruumi väljaspool kvantsüsteemi. Piiri kvantsüsteemi ja lahusti vahel nim molekulaarpinnaks. Kvantsüsteemi osalaengud polariseerivad kontiiniumi tema ümber ja see omakorda saab muuta kvantsüsteemi laengujaotust. SCRF algoritm arvutab reaktsioonivälja Poissoni või Poisson-Boltzmanni võrrandite lahendite abil ja iteratiivselt saavutab pidevuse reaktsioonivälja ja kvantsüsteemi laengujaotuse vahel.

SCRF on erinevad meetodid sõltuvalt molekuli kujust (sfäär, piklikud mol, rotatsiooniliselt painduvad molekulid)

Polariseeritava kontiiniumi meetod

Lahustisse moodustunud augu kuju saadakse lahustunud aine vdW raadiustest. Reaktsioonivälja kirjeldav potentsiaal esitatakse summana üle väikeste pinna elementide ja elementidele vastavate punktlaengute. See meetod on siis rakendatav igasugusele pinna kujule.

COSMO

Auk tehakse ülijuhti, millel on lõpmatult tugevad dielektrilised omadused. Juhul kui lahusti on ideaalne juht, siis elektriline potentsiaal soluudi ja solvendi pinnal kaob ära. Kui molekuli laengujaotus on teada, siis on võimalik ka arvutada laengut molekuli pinnal. Reaalsete lahustite korral erineb solvendi laeng pinnalaengust f korda?? Teades lahusti laengut ja molekuli laengujaotust on võimalik arvutada solvendi ja lahustunud molekuli interaktsiooni energiat. COSMO sobib hästi kõrget dielektrilist konstanti omavate keskkondade modelleerimiseks (vesi)

Molekulaarmehhanika alused. Jõuväljade mõiste ning nende arvutamine. Molekulaarmehhaanika rakendused ravimidisainis.

Molekulaarmehhaanika on robustne meetod keemilise molekuli energia arvutamiseks. Selles meetodis vaadeldakse erinevalt B-O lähendusele just tuumade liikumist, (elektronide jaotus on fikseeritud tuumade ümber ja seda iseloomustatakse parameetritega). Molekule esitatakse kui omavahel vedrudega seotud palle. MM põhimõtteline eelis on see, et arvutuslikult vähem ressursimahukas vrld kvantmeh meetoditega; võimaldab uurida molekulaarseid süsteeme, mille suurus on 1000 ja enama aatomi kandis.

Jõuväli: osakeste süsteemi potentsiaalset energiat kirjeldava matemaatilise funktsiooni kuju ja parameetrid. Jõuvälja kvaliteet sõltub olulisel määral pot energia liikmete konstantide parametriseerimisest.

Energiat vaadeldakse kui aatomite asendite funktsiooni.

Koguenergia= kovalentne energia + mittekovalentne energia

Kovalentne energia koosneb sidemete, sidemetevaheliste nurkade ja sid vah ruuminurkade energiast. Mittekovalentne koosneb van der Waalsi või elektrostaatilise vastasmõju energiatest.

Sidemete võnkeid ja tasapinnaliste nurkade võnkeid arvutatakse tavaliselt harmoonilise funktsiooni abil. (Esimest ka Morse fun abil, mis on täpsem, aga aeganõudvam)

Ruumilisi nurki ehk rotatsiooni arvestav liige esitatakse Fourier rittaarendusega

VdW esitatakse Lennart-Jonesi potentsiaaliga

Elektrostaatiline interaktsioon saadakse Kuloni seadusest

Vesiniksidemeid kirjeldav liige saadakse modifitseeritud L-J potentsiaaliga.

Rakendused: MM võimaldab kiirelt määrata molekulaarseid energiaid; teha konformatsioonianalüüsi; kiire 2D-3D konversioon.

Molekulide potentsiaalipinnad ja nende iseäralikud punktid (miinimumkohad ja sadulpunktid). Molekulide geomeetria optimiseerimine. Keemiliste reaktsioonide kiirus-ja tasakaalukonstantide teoreetiline arvutus.

Potentsiaalse energia pind kirjeldab molekuli energia muutu lähtudes tuumade positsioonide muutustest.

Statsionaarsed punktid, tingimus, et energia I järku tuletis reakts koord järgi = 0

Energia miinimum (lokaalne/globaalne); II järku tuletis on positiivne

Sadulpinna punktid: üks ja ainult 1 punkt negatiivne

(energia maksimum, II tuletis negatiivne)

Molekuli geomeetriat optimiseeritakse eesmärgiga:

Leida molekuli minimaalse energiaga geomeetriat

Ainult energial põhinevad algoritmid muudavad 1 koordinaati korraga; arvutus toimub üle kõigi koordinaatide (Fletcher-Powelli algoritm). Sellel meetodil on kõige laiemad kasutuspiirid, aga kõige aeglasem energia koondumine.

Gradienti kasutavad algoritmid: Eeliseks see, et on väga efektiivne, puuduseks, et ei tööta hästi lamedate tasapindade korral, ehk juhtudel, kus miinimum pole selgelt identifitseeritav- sellistel juhtudel on soovitatav kasutada energia II järku tuletisi.

Energia II järku tuletis: Newton-Raphson algoritm: peamine aktiveeritud komplekside leidmiseks. Eeliseks, et miinimum leitakse sisuliselt 1 sammuga; puuduseks, et arvutus võtab tunduvalt kauem aega.

Leida esimest järku maksimumi ehk sadulpinna punkti (aktiveeritud olekut)

Sadulpinna punkt peab olema min kõikides energia pinna suundades va 1, mille suunas on ta maksimum. Leidmiseks kasutatavad meetodid:

Pinna sobitamine : analüütilised võrrandid sobitatakse arvutatud energiatega, hoitakse ära kulukad MO arvutused. Halb on see, et puudub üldine meetod leidmaks sobivat fun vorm mitmedimensionaalsele pinnale. Vaja teha palju energia arvutusi, et saavutada piisavat sobivust

Koordinaadi juhitud üleminek:Eeliseks- lihtne kasutada; omab rakendusi paljudes kvantkeemia programmides. Puudused- kulukas; strateegia annab aktiveeritud oleku struktuuri ligilähedase esituse (mitte täieliku); arvutatud reaktsioonitee on ligilähedane ja ei tööta kumerate reaktsiooniteede korral.Veel: Orgu mööda üles jalutamine; Gradienti kasutavad meetodid, lineaarsed ja ruutsünkroonsed meetodid

visualiseerida kogu potentsiaalset pinda.

Keemiliste reaktsioonide kiirus-ja tasakaalukonstantide teoreetiline arvutus:

Tasakaalukonstant K reaktsioonile A → B arvutatakse

K = N_b/N_a =(q_b/q_a)exp(-?U(0)/k_bT), kus ?U(0) on A ja B siseenergia erinevus 0K juures; k_b-Boltzmanni konstant; T-absoluutne temperatuur ja q_b ,q_a B ja A molekulaarsed jaotusfunktsioonid (näitavad kuidas molekulid jaotuvad eri energiatasemete vahel)

Aktiveeritud kompleksi teooria 3 eeldust:

kõik molekulid, mis läbivad jaotava pinna moodustavad reaktsiooni produktid ja ei pöördu tagasi lähteolekusse

reagentide tasakaaluline jaotus säilib alati

molekulid eraldaval tasapinnal on alati termilises tasakaalus reagentidega

Kiiruskonstandi puhul vaadeldakse lähteainete ja aktiveeritud oleku vahelist tasakaalukonstanti. Seega reaktsiooni kiiruskonstant on k=(k_bT/h)K^#

Laengujaotus molekulides. Mullikeni laengujaotuse skeem LKAO MO meetodi raames.

Populatsiooni analüüs jaotab elektronide tiheduse tuumade vahel nii, et tuumaga on seotud teatud arv elektrone.

Korrutist P_mnS_mn nim tavaliselt Mullikeni populatsiooniks. Need esitavad iga AO korrutise panust molekuli elektronide koguarvu. Kui AO on normaliseeritud (S_mm=1), siis P_mm on populatsioon orbitalil φ_m. Kui kattumine AO-de vahel puudub (S_mn=0), siis kogu elektronide arv võrdub P_mm-de summaga. Tegelikkuses AO-d kattuvad ja seda väljendab korrutis P_mnS_mn

Mullikeni meetodi korral on kogu elektonide tihedus (P_mm) aatomorbitalil φ_m seotud aatomiga, mille juures ta asub. Ülejäänud elektronide tihedus on seotud kattuvate populatsioonidega (Iga tihedusmaatriksi elemendi φ_m φ_n pool tihedusest omistatakse aatomile, mille juures φ_m asub ja teine pool aatomile, mille juures φ_n asub.

Kogulaeng aatomil A arvutatakse siis lahutades aatomi laengust elektronide arvu aatomil.

Suurim puudus on see, et tulemus sõltub väga baasifun valikust (baasifun peavad olema balansseeritud).

Orbitaalne sümmetria ning Woodward-Hoffmanni reeglid. Lubatud ja keelatud fotokeemilised ja termilised reaktsioonid (tsüklobutaani ja tsüklohekseeni tekkereaktsioonid).

Keemilised reaktsioonid

toimuvad kui reagentide ja produktide orbitalid ühilduvad ja nad on sümmeetrilised

toimuvad raskustega kui ühildumist pole

Lubatud on reaktsioonid, mis sarnased Diels-Alderi reakts ja kus puudub korrelatsioon siduvate ja lõhustavate nivoode vahel. Neid kirjeldatakse kui orbitaalse sümmeetria poolt lubatud reaktsioone statsionaarsete olekute vahel ja sümmeetria poolt keelatud reaktsioone ergastatud olekute puhul.

Keelatud on need, mis sarnanevad etüleenide vahelisele reaktsioonile ja näitavad siduvate-lõhustavate nivoode vahelist korrelatsiooni ja on seega sümmeetria poolt keelatud reaktsioonid stats olekute vahel ja sümm poolt lubatud reaktsioonid ergastatud olekutes.

TSÜKLOBUTAAN JA TSÜKLOHEKSEEN

Molekulaardünaamika ja selle rakendused korrapäratute kondenseeritud süsteemide kirjeldamisel. Monte Carlo meetod.

Molekulaardünaamika eesmärk on solvendi (kondenseeritud süsteemi) kirjeldamine. Jaguneb kaudseteks (nö kontiinumi) mudeliteks ja täpseteks mudeliteks

Kaudsed mudelid arvutavad süsteemi koguenergia E_tot=E_kovalentne+E_mitte-kov+E_{solvatatsioon} Lihtsaim viis solvendi mõju arvestamiseks E_mitte-kov = summa laengute korrutistest jagatud dielektrilise konstandiga. Solvatatsiooni energia saab arvutada solvatatsiooni vabaenergiast.

Täpsetes mudelites jõuvälja lisaliikmeid ei panda, vaid defineeritakse parameetrid vee molekulidele. Täpsed mudelid jagunevad omakorda:

lihtsad: interaktsioonikohad on määratud, vee molekulid on jäigad, vastasmõjud molekulide vahel on kirjeldatud paarsete kuloniliste ja LJ potentsiaalidega

paindlikud: võimaldavad konformatsioonilisi muutusi vee molekulides

polariseeritava vee mudel: mittehomogeensetele süsteemidele, ioonid (ja ka muud laetud rühmad), mis põhjustavad elektrivälja gradiente.

Süsteemi lihtsustamiseks defineeritakse ühikrakud, mis asetatakse perioodiliselt üksteise kõrvale ja lõpuks ongi uuritav molekul igalt poolt ümbritsetud solvendimolekulidega. Pinna modelleerimisel kasutatakse perioodilisi piirtingimusi ja mitte-perioodilisi näiteks mingi ensüümi uurimiseks solvendis.

Monte Carlo meetod loob konformatsioone juhuslikult

liigutades üksikut aatomit või molekuli

liigutades korraga mitut aatomit, molekuli või pööratakse 1, mitut sidet.

MC kasutab kriteeriumide komplekti uute konformeeride aktsepteerimiseks Need kriteeriumid kinnitavad, et antud konf saamise tõenäosus võrdub Boltzmanni faktoriga exp(-V(r^N)/k_bT). Kus V(r^N) on arvutatud kasutades potentsiaalse energia funktsiooni. Seetõttu madalama energiaga olekuid genereeritakse suurema tõenäosusega kui kõrgema.

Kui saadud energia on madalam kui eelkäijal, siis võetakse uus konfiguratsioon vastu; kui saadud energia on kõrgem , siis arvutatakse energiate erinevuse Boltzmanni faktor, genereeritakse juhuslik arv 0 ja 1 vahel ja võrreldakse seda B faktoriga, kui juhuslik arv on suurem B faktorist, siis konformatsioon elimineeritakse ja kasutatakse eelmist; kui juhuslik arv väiksem B faktorist, siis konf aktsepteeritakse ja on süsteemi järgmine olek.

Seega MC meetod võimaldab samme kõrgema energia suunas.

Kvantitatiivsete sõltuvuste leidmine molekulide struktuuri ja nende omaduste (füüsikalised omaduse, keemiline reaktsioonivõime, bioloogiline aktiivsus) vahel. Empiiriline ja teoreetiline lähenemine kvantitatiivsetele struktuur-aktiivsus-omadus sõltuvustele (QSAR/QSPR). Vaba energia lineaarsused

QSAR s eob molekuli struktuuri arvulised omadused selle aktiivsuse (või omadustega) matemaatilise mudeli kaudu. Struktuur-aktiivsus sõltuvuste uurimine võib anda aimu, millised molekuli omadused mängivad suuremat rolli tema üldise bioloogilise vm aktiivsuse juures

Empiiriline lähenemine tähendab seda, et kasutatakse enamuses eksperimentaalselt saadud deskriptoreid (struktuursed- induktsioon, resonants, steeriline; solvatatsioon-polaarsus, polariseeritavus, happelisus..), teoreetilises lähenemises kasutatakse arvutuslikult saadud molekuli struktuuri kirjeldavaid deskriptoreid (laengujaotust kirjeldavad, kvantkeemilised, geomeetrilised..)

LFER füüsikalises orgaanilises keemias seovad kvantitatiivselt molekuli struktuuri ja ta omaduse, aktiivsuse (kiirus või tasakaalukonstandi).Tafti ja Hammeti substituendikonstandid

Näiteks kui on konkreetne reaktsioon 2 molekuli vahel. Tehakse seeria reaktsioone, kus ühte reagenti muudetakse veidi (näiteks viiakse molekuli asendajaid erineva elektronegatiivsusega). Koos muutuva reagendiga muutub ka reaktsiooni kiirus ja tasakaalukonstant.

Kui 1 reagendi muutmine samal viisil mõjutab mõne teise reaktsiooni kiirus ja tasakaalukonstanti samamoodi, kui mõjutas muutmine esimese reaktsiooni oma, siis saab öelda, et on olemas lineaarne vaba energia sõltuvus 2 efekti vahel. Selliste sõltuvuste abil saab hinnata reaktsioonimehhanisme ja ennustada tasakaalukonstante.

Keemiliste ühendite empiirilised elektroonsed ja steerilised substituendikonstandid ja solvendi parameetrid.

Empiirilised elektroonsed substituendikonstandid kirjeldavad elektroonseid interaktsioone molekulis. Tähtsamad:

Hammeti substituendikonstant- väljendab vähemalt 2 molekulisisest interaktsiooni: induktsioon, resonants

konstandid läbiva resonantsi kirjeldamiseks

Tafti konstant- kasutusel kui läbiv resonants on blokeeritud (alifaatsete ühendite korral)

induktsiooni elektroonne osakaal aromaatsetes süsteemides

Resonantsi elektroonne panus Tafti konstandile

induktsiooni elektroonne osakaal alifaatsetes süsteemides

Steerilist interaktsiooni kirjeldavad substituendid

Tafti steerika parameeter

minimaalne topoloogiline erinevus

molaarne refraktsioon

Lahustumise parameetrid:

polaarsuse skaalad: lahusti dielektriline polarisatsioon lahustunud molekuli väljaspool

polariseeritavuse skaalad: lühiajalised lahusti elektronide ja tuumade vahelised polariseeritavuse efektid välises elektrilises välja

Aluselisuse skaalad; happelisuse skaalad: lahusti käitub kui H-sideme doonor/aktseptor

Keemiliste ühendite teoreetilised konstitutsioonilised, topoloogilised, geomeetrilised ja elektrostaatilised molekulaardeskriptorid. QSAR/QSPR mudelite leidmine suurte deskriptorbaaside korral.

Konstitutsioonilised deskriptorid on enamasti lihtsalt loetelud (aatomite koguarv, absoluutsed ja suhtelised aatomite arvud, sidemete arv, molekulmass jne)

Topoloogilised deskriptorid toetuvad enamuses graafi teooriale; kirjeldavad molekuli hargnemist, ruumilist ulatust, ja paindlikkust: Wieneri indeks; Kier ja Halli indeksid

Geomeetrilised deskriptorid kirjeldavad molekuli kuju ja sellega seotud omadusi nagu molekulaarruumala; -pindala jne.

Laengujaotust kirjeldavad deskriptorid pärinevad empiirilistest skeemidest või kvantkeemia arvutustest: dipoolmoment, osalaengud, polariseeritavused.

Deskriptoreid valitakse 4 põhimõtte alusel:

deskriptorite väärtused peavad pärinema ühest ja samast allikast (mõõdetud 1 tüüpi eksperimendiga, arvutatud ühe ja sama tarkvaraga)

deskriptorite arv võrrandis tuleb viia miinimumini ilma informatsiooni kaota (väljendatuna erinevate statistiliste kriteeriumitega)

multilineaarse regressioonimudelites peavad deskriptorid olema ortogonaalsed

deskriptori füüsikaline/keemiline sisu peab olema sarnane uuritava omaduse/nähtusega

Deskriptorid ei tohiks korreleeruda, see tähendaks, et nad kirjeldavad sama efekti.

Ühe deskriptori kohta peaks olema vähemalt 5 andmepunkti; vastasel juhul on juhustliku korrelatsiooni võimalus liiga suur

Suurte deskriptorbaaside korral kasutatakse astmelise regressiooni meetodeid:

heuristiline

parima multi-lineaarse regressiooni meetod

JOONISTA HEURISTILINE